前些天,OpenAI 研究员宣称 GPT-5 「发现」了 10 个悬赏数学难题的解决方法,舆论误以为是 GPT-5 给出了解题方法,结果被发现只是检索到了早已存在的文献,引发了学界大佬的群嘲以及对于 AI 领域夸大宣传和 AI 检索能力的激烈讨论。参阅报道《OpenAI「解决」10 道数学难题?哈萨比斯直呼「尴尬」,LeCun 辛辣点评》。
然而,讽刺的是,当人们还在辩论 AI 是不是一个合格的「文献检索员」时,真正的数学发现已经悄然发生。
AI 取得研究突破
加州大学洛杉矶分校(UCLA)数学教授 Ernest Ryu 发推称:「我使用 ChatGPT 解决了凸优化中的一个未曾被解决的问题。」

随后,他通过一系列推文介绍了自己与 ChatGPT 的联合成果。
首先来看一下他所研究的问题本身:

呃,看不懂,但我们可以让 AI 来帮助我们理解(AI 再立大功!):
这个数学问题探讨的是一个在最优化理论中非常著名的动态系统,我们可以用一个生动的物理比喻来理解它:一个球在碗里的滚动过程。在这个比喻中,被称为「凸函数」的 f 就代表一个形状完美的碗,它内部光滑,从碗边到碗底的坡度是逐渐下降的,没有任何凹陷或小山丘。这个碗的碗底可能是一个尖锐的点,也可能是一片宽广的平坦区域,这片最低的区域在数学上被称为 argmin f。而 X (t) 则描述了在时间 t 时,一个球在这个碗中所处的位置。截图中的那个核心微分方程,Ẍ(t) + (3/t)Ẋ(t) + ∇f (X (t)) = 0,就是控制这个球如何滚动的「物理定律」。其中,∇f (X (t)) 扮演了「重力」的角色,时刻将球往坡度最陡峭的下方拉扯;而 (3/t)Ẋ(t) 则是一个非常特殊的「摩擦力」,它的奇特之处在于会随着时间的流逝而逐渐减弱。一开始摩擦力很强,能有效减速,但随着时间 t 变得越来越大,这个摩擦效应会变得越来越微弱。整个问题就是从碗壁的某个初始位置 X₀ 将球从静止状态释放,然后观察它在这套独特的物理规则下将如何运动。
这个问题的真正核心与挑战,在于需要严格证明:这个滚动的球最终不仅会到达碗底,而且会完全静止在碗底的某一个确切的点上。表面上看,这似乎是理所当然的,但在数学上却是一个深刻的难题。数学家们早已证明,球的「高度」 f (X (t)) 随着时间的推移,必然会无限趋近于碗底的最低高度。换言之,我们 100% 确定这个球最终会进入碗底的最低区域,而不会停在半山腰。但这仅仅是「函数值收敛」。真正的「悬而未决的难题」在于球的「位置」 X (t) 是否也会收敛。如果碗底是一个宽广的平坦区域,球在到达这个区域后,会不会因为惯性而永无止境地滑行、振荡或者兜圈子,就像一个陀螺在光滑的地面上不停旋转一样?这个问题要求证明,恰恰是由于那个 3/t 的特殊时变摩擦力,它能以一种恰到好处的方式耗尽球的所有动能,最终引导它停泊在一个固定的位置上,而不是在最低能量状态下进行永恒的漂移。这在很长一段时间里都是一个吸引了众多研究的公开问题,因为它触及了优化算法收敛性理论的基石。
下面则是 ChatGPT 的证明,但也经过了 Ernest Ryu 教授的整理:


他也分享了原始的交互记录:https://chatgpt.com/share/68f805f2-b8fc-8010-8df6-20a46bc1df44
从这份记录可以看到,他使用的模型是 GPT-5 Pro,而该模型为该问题执行了 22 分钟的推理。

同样,AI 基于此给出的分析是:Nesterov ODE (常微分方程) 的解 X (t) 最终会收敛到函数 f 的某一个最小值点 X∞。
我们也能在证明中看到 z₁ 和 z₂ 距离为 0,意味着这两者必须是同一个点。这与最初「假设存在两个不同的点」相矛盾。因此,最初的假设是错误的,所以这个球只能停在一个点上。
Ernest Ryu 还介绍了自己的历程和想法:「我的反应:ChatGPT 确实有效地加速了我的进度。这项工作花了大约 12 个小时,分 3 天进行。现在回想起来,证明过程其实很简单。」
他继续介绍说:「但我尝试了许多其他策略,但都没有成功,而 ChatGPT 至关重要地帮助我快速探索并消除了这些死胡同。此外,关键的成功步骤也是由 ChatGPT 提出的。」
不过他也指出,ChatGPT 的成功并不是一蹴而就的:「ChatGPT 并非一次性给出证明。整个过程高度互动。它提出了许多论点,其中大约 80% 都是错误的。但有些想法对我来说确实很新颖。每当我意识到一个新奇的想法,无论正确与否,我都会提炼出其中的关键洞见,并促使 ChatGPT 对其进行进一步的开发。」
Ryu 还总结了自己与 ChatGPT 各自的贡献:
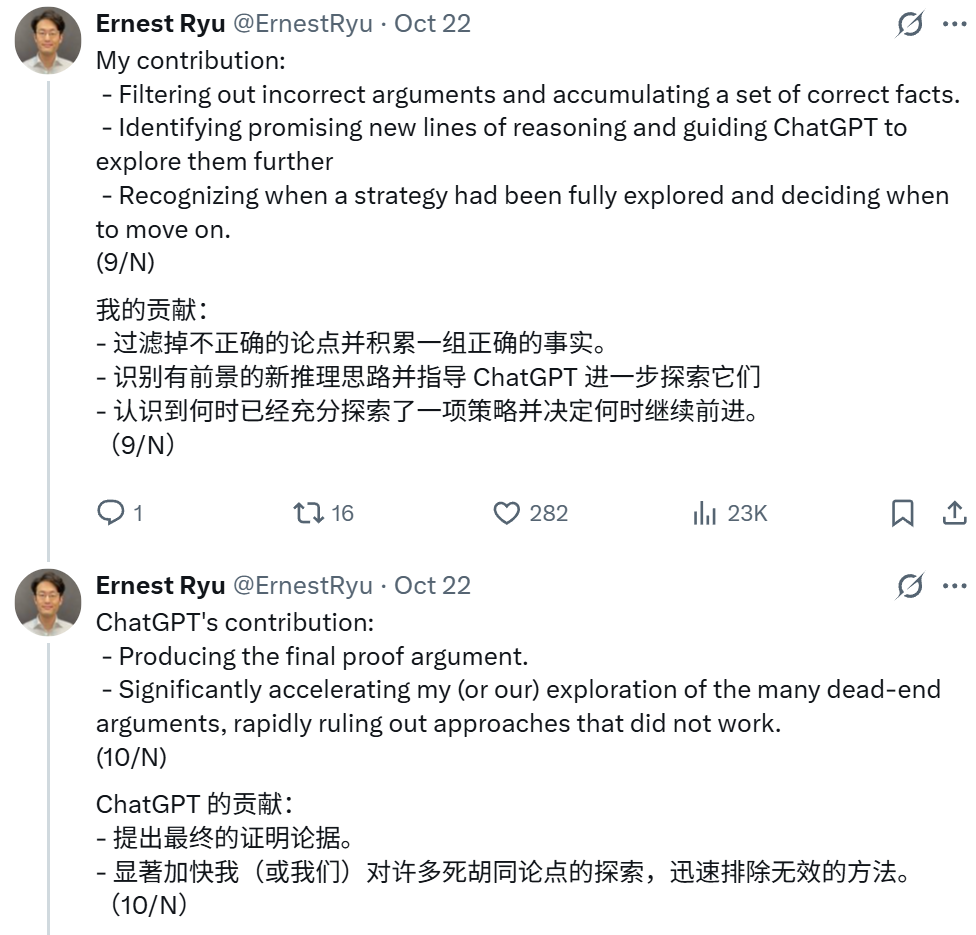
最后,他指出:「在我看来,这个结果已经可以在权威的优化理论期刊上发表。不过,我还想进一步完善它。」未来他还计划将该证明泛化到 r>0 的 ODE 以及尝试「将这个论证转化为证明离散时间对应方法(即 Nesterov 加速梯度法)的收敛性」。
他总结说:「ChatGPT 现在已经处于能解决一些数学研究问题的水平,但确实需要一位专家来指导它。」
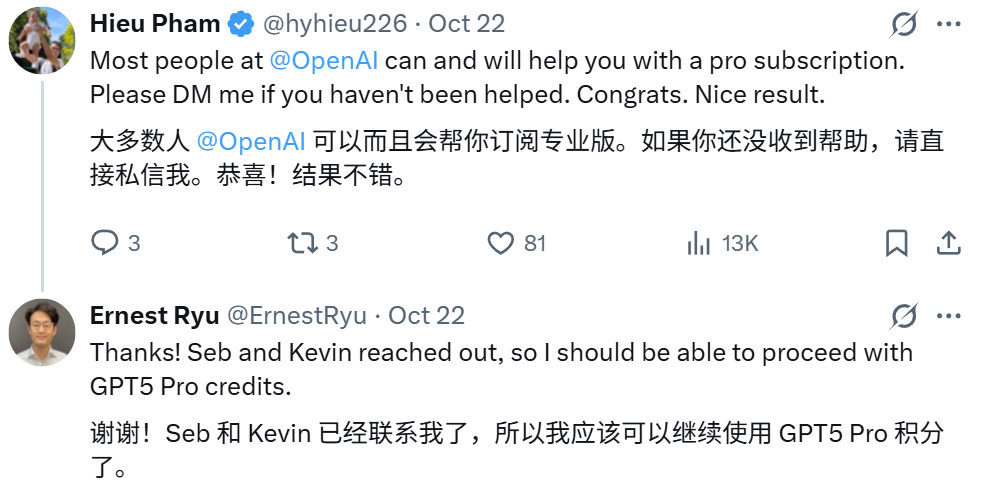
有意思的是,他提到自己研究过程中最大的障碍是「用完 ChatGPT Pro 查询」,而他使用的已经是「昂贵的 Pro 计划」,只能等下个月刷新了。
当然,这是个相当不错的宣传机会,已经有 OpenAI 工作人员联系他,并提供了更多积分。
AI 成为论文第一作者
无独有偶,加州大学欧文分校(UCI)数学教授 Paata Ivanisvili 前些时日也宣称 GPT-5 Pro 助其发现了一个命题的反例。
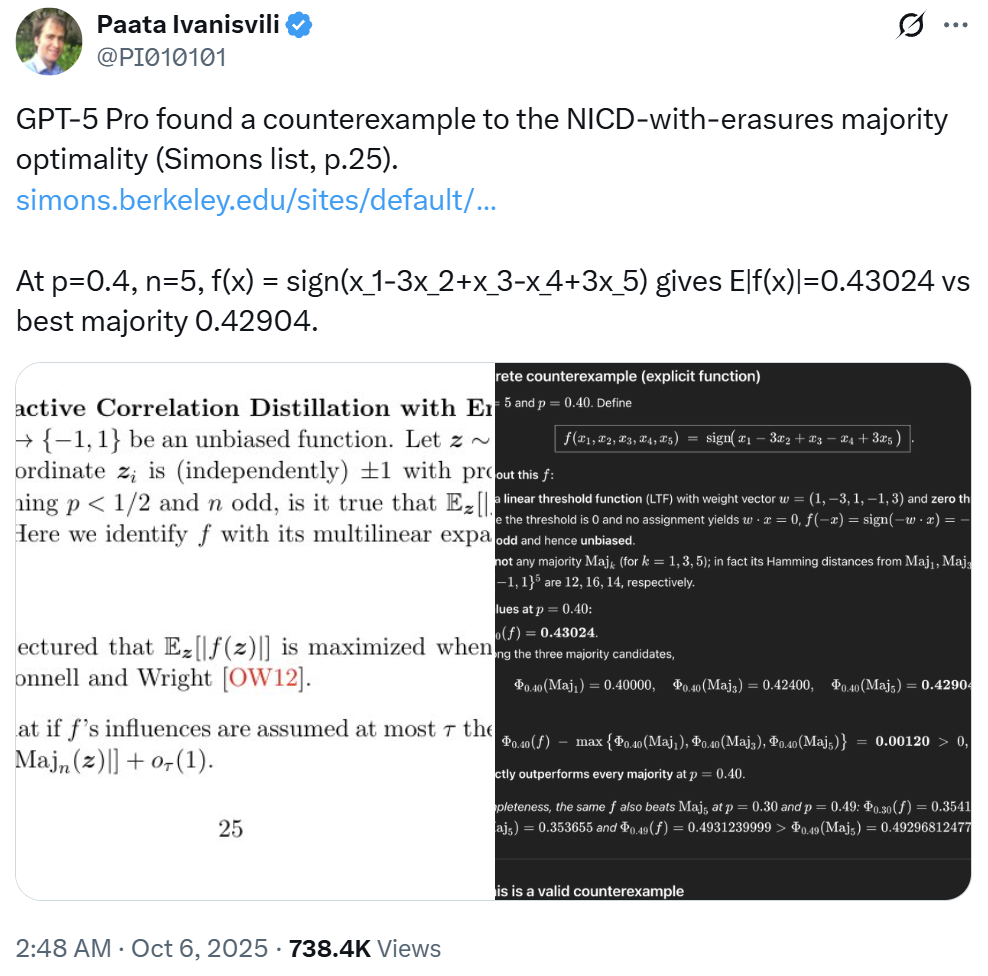
更有趣的是,他刚刚还宣布要将 ChatGPT 列为他这篇论文的合著者,并且还是第一作者!

当然,这早已不是 AI 首次以作者身份登上严肃的学术论文,早在 2023 年 ChatGPT 就已经当作论文第三作者,参阅报道《一位论文作者火了,ChatGPT 等大型语言模型何时能成为论文合著者?》不过,值得注意的是,该论文的最新版本的作者名单中已经没有 ChatGPT 的身影。

2023 年的截图,现如今该论文的作者名单中已经没有 ChatGPT
AI 辅助证明,成为第二作者
而在前些天的所谓「OpenAI『解决〗10 道数学难题?」事件之后,有两位人类研究者遭遇了类似的尴尬。他们在宣布成功解决了 #707 Erdos 问题之后发现这个问题其实 30 年前就已经被解决了!
不过他们也并未止步于此,而是继续让 GPT-5 编写了一个 Lean 形式化证明,并成功进行了验证。当然,他们也强调了专家指导和反馈的重要性。
总之,我们看到,在其论文的作者列表中,ChatGPT 与 Lean 都跻身其中。

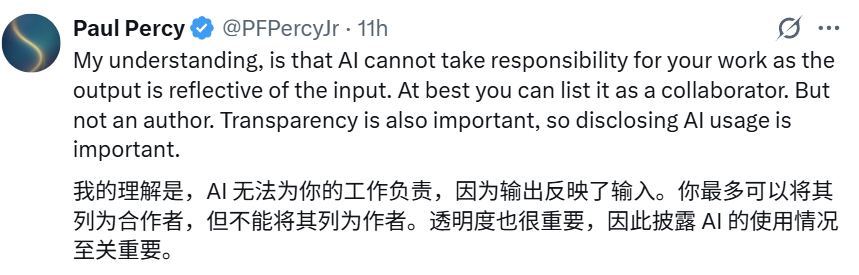
当然,将 AI 列为论文作者的做法依然存在巨大争议。


结语
顺带一提,在前述相关推文的评论区,我们也能看到其它一些使用 AI 取得研究进展的信息:
Ernest Ryu 教授的故事,连同其他研究者的经历,共同揭示了一个正在到来的新时代:AI 或许不再仅仅是工具,它正在成为研究伙伴。
这意味着,未来顶尖的科研,或许将不再是单打独斗的英雄主义,而是人类专家与强大 AI 之间的深度对话与协作。
那么,屏幕前的你呢?你有在自己的研究工作中使用 AI 吗?体验如何?欢迎分享你的故事。



